整数规划
Table of Contents
#线性规划
定义&特性 #
对决策变量有整数要求的数学规划问题(线性/非线性).
- 有广泛的应用背景, 如指派问题、背包问题、旅行推销商问题都是整数规划问题.
- 是最难求解的问题之一, 至今还没有找到有效算法.
整数规划与线性规划的联系 #
- 整数规划 = 相关的线性规划 + 整数约束;
- 整数规划是约束得更紧的问题, 它的可行域是其相关线性规划问题可行域的一个子集.
- 整数规划的求解难度远大于线性规划.
整数规划的分类 #
- 纯整数规划: 所有决策变量取整数值;
- 0-1整数规划: 整数变量只能取0或1;
- 混合整数规划: 部分决策变量取整数值或二态值.
整数规划求解的困难性 #
问题1 #
- Q: 为什么不求解对应的线性规划问题, 然后将解四舍五入取整数解呢?
- A: 如下图所示, 在部分可行域中, 整数规划最优解可能与线性规划最优解相差甚远.
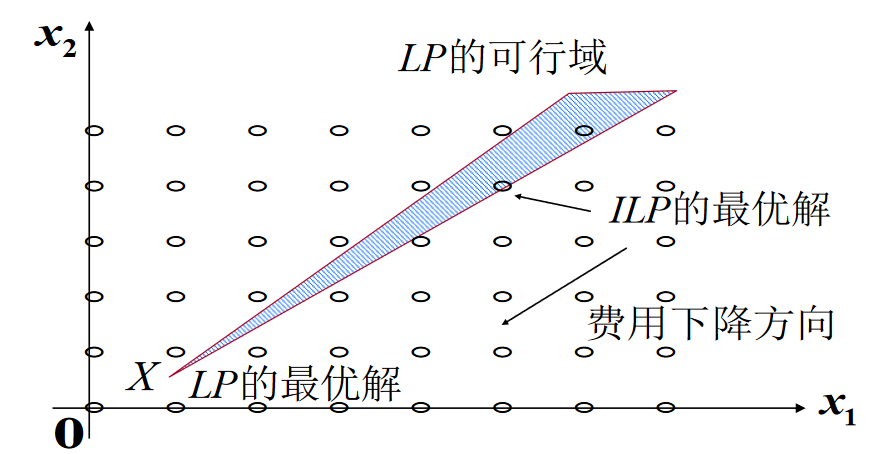
问题2 #
- Q: 可以使用枚举法来求解整数规划问题吗?
- A: 当数据量较小时是可以的. 但对于一般的整数规划问题, 枚举法的计算量通常呈指数级增长态势, 即使是计算机也无能为力.
如何克服其困难性? #
- 割平面法: 有理论意义, 但计算效率较低;
- 分支定界法: 剪枝, 计算效率高, 应用广泛;
- 隐枚举法: 需要精心设计;
- 启发算法: 效率高, 但不保证能够找到最优解, 可以解大规模问题
割平面法 #
考虑纯整数规划问题:
$$
max\ z = \sum_{i=1}^{n}c_ix_i\
s.t.
\begin{cases}
\sum_{j=1}^{n}a_{ij}x_j\leq b_i, (i=1,…,m)\
x_j\geq 0, (j=1,…,n)\
x_j取整数
\end{cases}
$$
割平面法的基本思想: 先求解松弛问题.
设松弛问题的最优解 $X^=(x_1…x_m\ y_1…y_n)$ , 其中基变量为 $(x_1…x_m)$ , 非基变量 $(y_1…y_n)$
假设 $X^$ 不是整数, 考虑某个不为整数的 $b_i$ 对应的诱导方程:
$$
x_i+\sum_{j=1}^n\overline{a}{ij}y_j=\overline{b}i
$$
其中, $\overline{b}i=\widetilde{b}i+\beta_i$,$\overline{a}{ij}=\widetilde{a}{ij}+\alpha{ij}$ .($\widetilde{b}i与\widetilde{a}{ij}$为整数, $\beta_i\in (0,1), \alpha{ij}\in [0,1)$).
诱导方程变形后即有:
$$
\beta_i - \sum_{j=1}^na_{ij}y_j=x_i-\widetilde{b}i + \sum{j=1}^{n}\widetilde{a}{ij}y_j
$$
注意到 $x_i-\widetilde{b}i + \sum{j=1}^{n}\widetilde{a}{ij}y_j$ 为整数,割平面方程即为:
$$
\beta_i - \sum_{j=1}^na_{ij}y_j+s_i=0
$$
其中$s_i$为非负整数.
该割平面方程满足:
- 没有割去任何一个可行的整数解;
- 割去了非整数最优解(当前松弛LP问题的最优解)
- 割平面法相当于一步步缩小可行域, 求解新的线性规划问题, 直到线性规划问题的最优解恰为整数, 这时便得到了原始整数规划问题的最优解;
- 割平面法只适用于纯整数规划问题.
分支界定法 #
考虑纯整数规划问题: $$ max\ z=CX\ s.t.\begin{cases} AX=b\ X\geq 0\ x_1,x_2,…,x_k为整数 \end{cases} $$ 其松弛问题为: $$ max\ z=CX\ s.t.\begin{cases} AX=b\ X\geq 0 \end{cases} $$ 求解该松弛问题, 如果最优解已经满足 $x_1,x_2,…,x_k$ 为整数, 则该解也是原整数规划问题的最优解;否则,我们选取$x_1,x_2,…,x_k$中的一个非整数分量 $x_i$ , 假设 $x_i$的取值在两个相邻整数$b_i$和$b_i+1$之间, 将松弛问题划分为子问题 $1$ : $$ max\ z=CX\ s.t.\begin{cases} AX=b\ x_i\geq b_i+1\ X\geq 0 \end{cases} $$ 与子问题 $2$ : $$ max\ z=CX\ s.t.\begin{cases} AX=b\ x_i\leq b_i\ X\geq 0 \end{cases} $$ 这相当于在松弛问题可行域中割掉了 $b_i<x_i<b_i+1$ 的部分(显然这一部分不会存在满足原整数规划的解). 求解子问题的过程中, 需要通过分支定界法继续分割问题.在这一过程中, 所求得的子问题最优解不一定是原问题最优解, 我们需要比较所有子问题的理论最有解才能得出原问题最优解.
分支变量选择原则
- 按目标函数系数:选系数绝对值最大变量先分支
- 按使用者经验来对各整数变量排列优先顺序
分支节点选择原则
- 深探法: 尽快找到整数解, 解的质量可能一般;
- 广探法: 选择目标函数当前最大值节点继续分支, 解的质量通常较高.
实践中有一种可行的剪枝方法, 当一个子问题不满足整数约束的最优解 $<$ 当前所得最优整数解时, 不必再在这一部分继续分支, 因为分支所得整数解不会取代当前最优整数解.
分支界定法优点
- 纯整数规划及混合整数规划都可以使用
- 思路简单灵活
- 速度快
- 适合上机