关键路径分析 #

一个项目可能包含多个活动 (activity), 每个活动需要一定的时间来完成, 同时活动之间可能存在依赖关系, 即某些活动是另一些活动的前提. 如果项目是线性进行的 (同一时间只能进行一项活动), 那么拓扑排序可以给出完成项目的路径, 并且计算总时长. 但如果项目中的活动能够并行运行, 那么如下两个问题很关键:

• 完成项目的最短用时是多少?
• 怎样才能尽可能多地并行?

活动点图 #

活动点图 (Activity-Node Graph) 是对上述项目的抽象. 每个节点是一个活动 (项目的开始和结束也视作活动) , 点权是完成活动所需的时间, 有向边代表活动间的依赖关系.

活动点图非常直观, 但依据它计算项目的最短用时相对复杂. 为此, 我们需要做一些变换.

事件点图 #

不同于活动点图, 事件点图 (Event-Node Graph) 中的节点代表活动的完成 (一个活动的完成也代表后继活动的开始) , 点之间的有向边代表了活动的依赖关系, 边权是完成活动所需的时间.

将活动点图转化为事件点图时, 如果一个活动有多个前提活动, 那么额外设置一个虚拟点 (可以视作 “前提活动全部完成, 该活动开始”) 作为该活动的前提, 虚拟节点与前继节点之间的边权记为 $0$ .

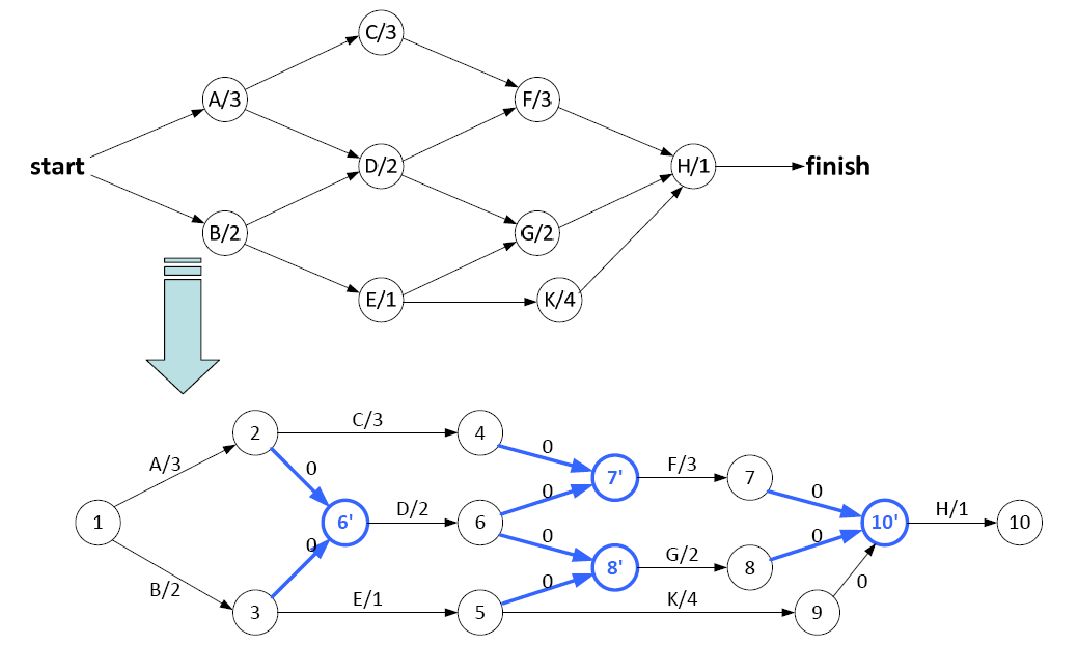
关键路径分析 #

关键路径分析 (Critical Path Analysis) 基于事件点图, 我们需要找到从项目开始到项目结尾的最长路径, 这条路径被称为关键路径, 这是因为整个项目的最短时间 $=$ 并行路径中最长的那一条.

最短完成时间 #

记 $EC_i$ 为节点 $i$ 的最短完成时间, 用如下方法计算所有节点的最短完成时间:

• $EC_1 = 0$
• $EC_w=max(EC_v + c_{v,w}),\ for\ all\ (v, w)\in E$

即一个节点的最短完成时间等于前置条件最短完成时间中的最长的.

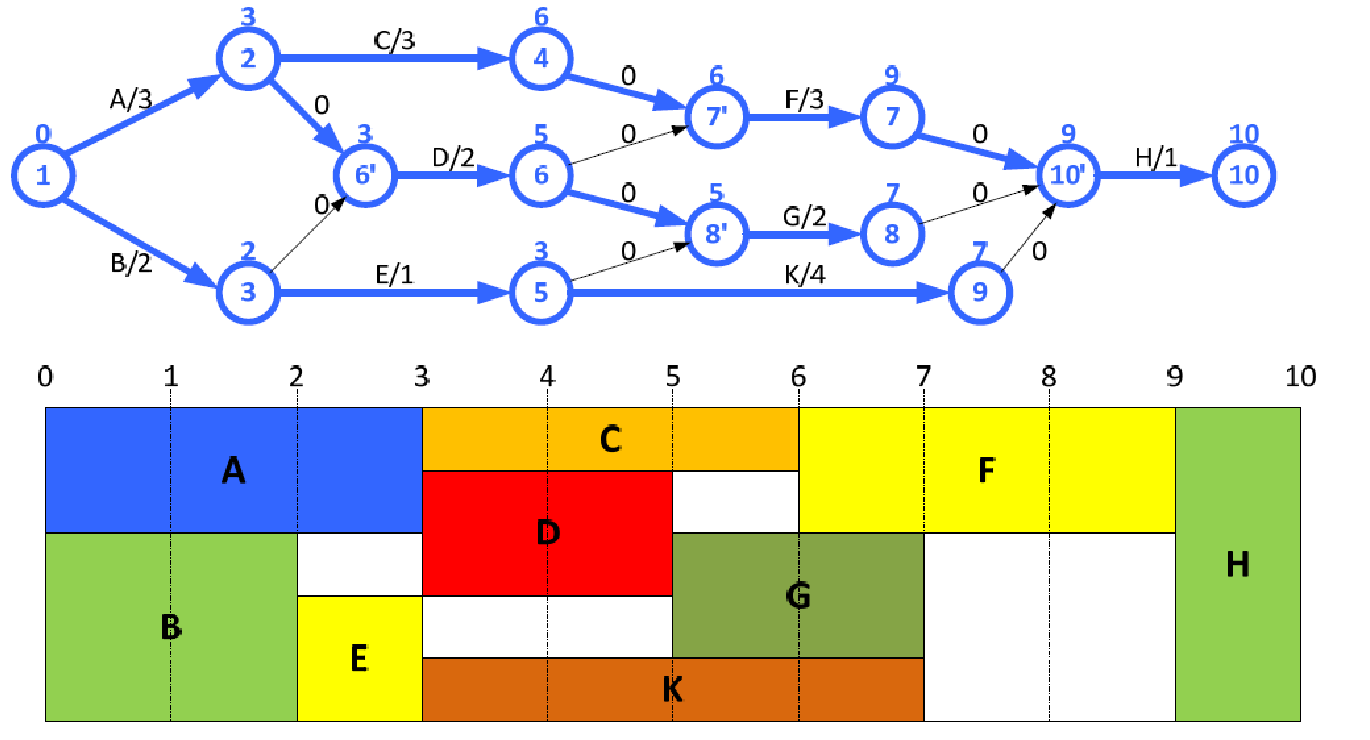
上面图片的下半部分直观地展示了整个流程. 从中可以看到, $A\rightarrow C\rightarrow F\rightarrow H$ 是一条关键路径, 必须马不停蹄地进行; 而 $B\rightarrow E\rightarrow K\rightarrow H$ 的时间要求则宽松很多. 想象一下把整个矩形框顺时针旋转 $90°$ , 所有的方块在重力的影响下向下坠落, 最终我们会得到一个最为 “拖延” 项目流程, 在不影响整体时间的情况下, 每个活动都尽可能慢地完成.

最长完成时间 #

重申一下, 这里的最长完成时间是在项目以最短时间完成的情况下, 每个活动的最长完成时间. 记 $LC_i$ 为节点 $i$ 的最长完成时间, 用如下方法计算所有节点的最长完成时间:

• $LC_n = EC_n$
• $LC_v = min(LC_w - c_{v, w},\ for\ all\ (v, w)\in E$

即一个节点的最长完成时间等于后继节点最晚开始时间中最短的.

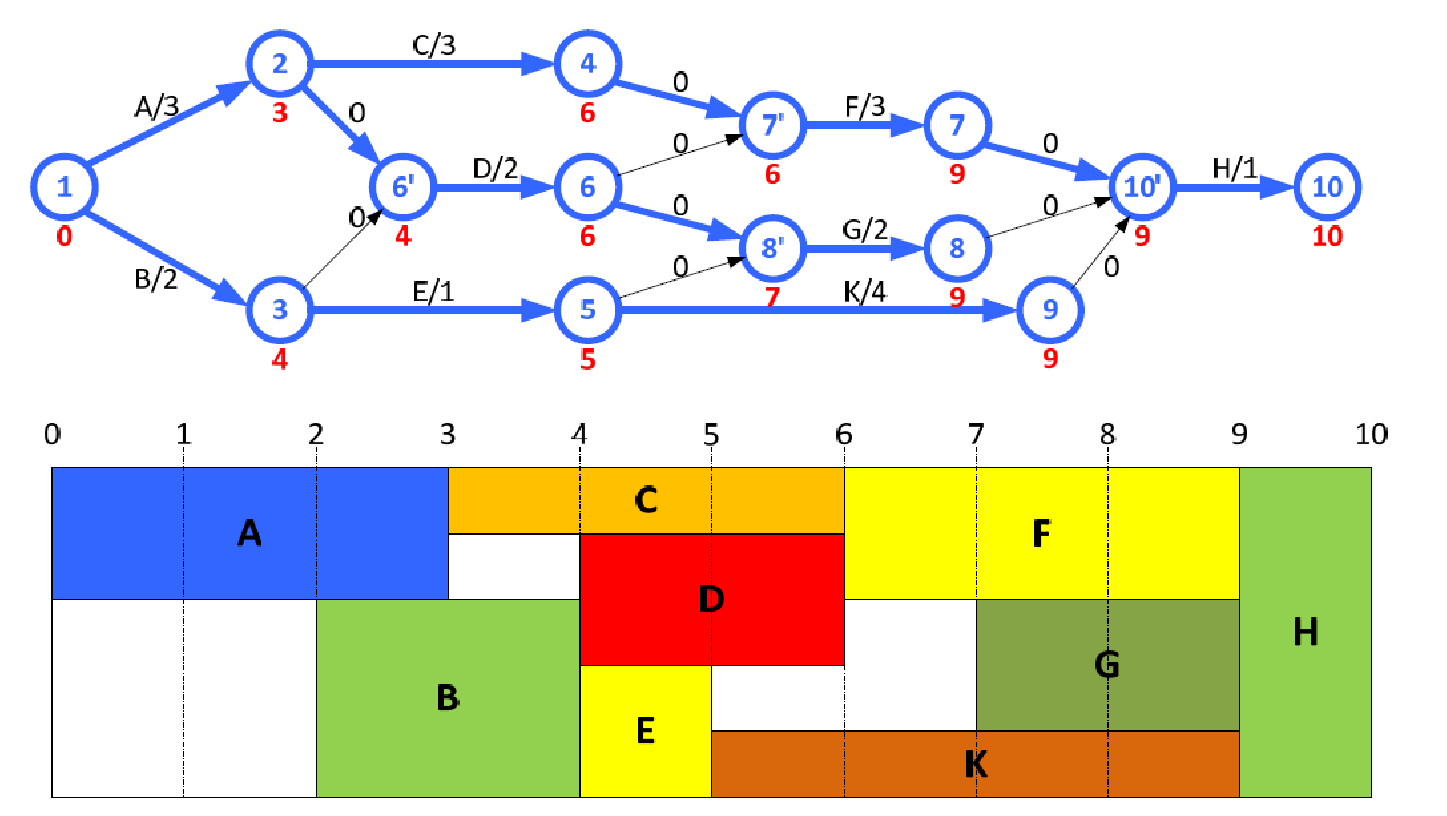
松弛时间 #

松弛时间 (Slack Time) 代表在项目以最短时间完成的情况下, 每个活动最多可以拖延的时间. 记 $Slack(v, w)$ 为 $(v, w)$ 代表的活动的松弛时间, 可以用如下方法计算:

• $Slack(v, w)=LC_w - EC_v - c_{v, w} = LC_w - EC_w = LC_v - EC_v$

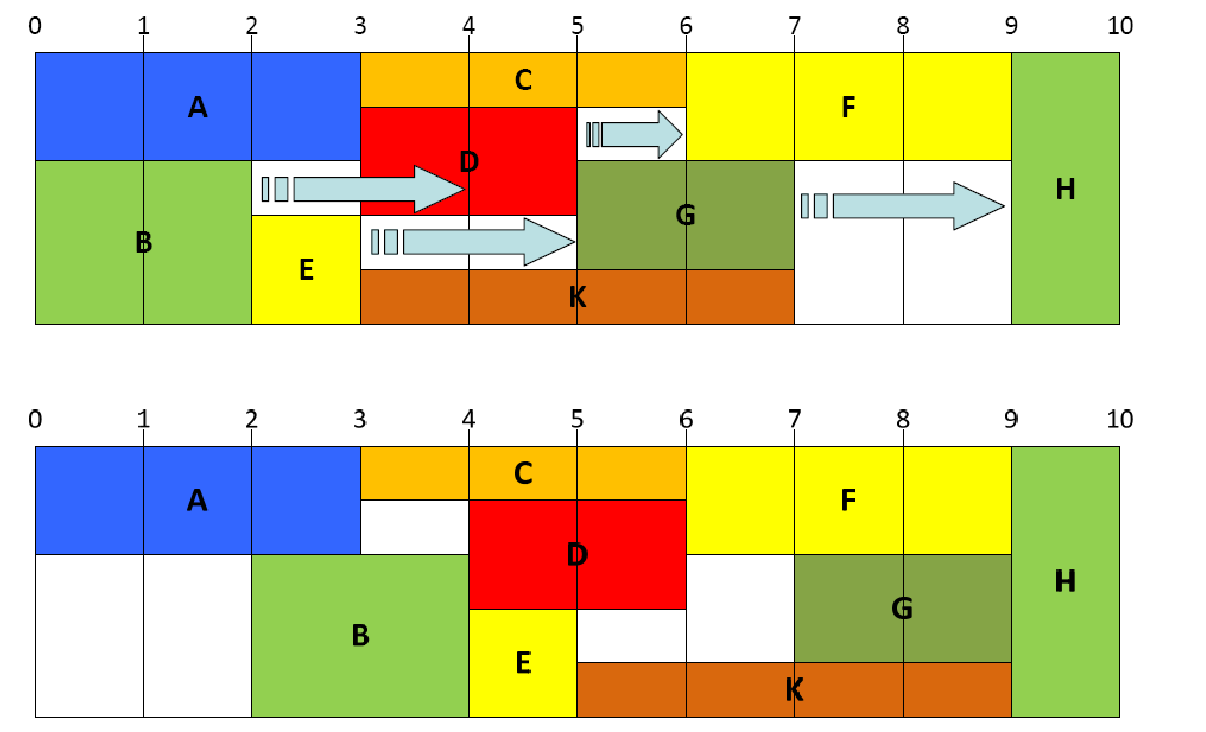
计算复杂度 #

关键路径分析的计算复杂度为 $O(\vert E+V\vert)$ .