↓Skip to main content
  1. Posts/

树状数组

·2 mins·
Table of Contents

树状数组 #

引入 #

对于一个数组, 最常见的操作有两种: 单点修改与区间查询. 对于常规数组而言, 单点修改的时间复杂度是 $O(1)$ , 但区间求和的时间复杂度是 $O(n)$ ; 如果使用前缀和来维护数组, 区间求和的时间复杂度是 $O(1)$ , 单点修改的时间复杂度则增长到了 $O(n)$. 如果既需要单点修改又需要区间查询, 显然这两种数据结构都不够好, 它们在某一特定方面表现得非常糟糕. 因此, 我们需要寻找这样一种数据结构, 它相对均衡, 在单点修改与区间查询方面都做得不错.

代码实现与分析 #

先看看树状数组的代码实现:

//定义lowbit()函数, 返回二进制数最右边的一个1及其后面的0
#define lowbit(x) ((x) & (-x))

// 全局变量数组
int tree[MAXN];

//单点修改&初始化操作, 将tree[i]修改为x, 
inline void update(int i, int x)
{
    for (int pos = i; pos < MAXN; pos += lowbit(pos))
        tree[pos] += x;
}

//求前n项和
inline int query(int n)
{
    int ans = 0;
    for (int pos = n; pos; pos -= lowbit(pos))
        ans += tree[pos];
    return ans;
}

//区间查询操作, 求第a, a + 1,..., b项之和
inline int query(int a, int b)
{
    return query(b) - query(a - 1);
}

核心项为三块:

  • $lowbit()$ 函数
//定义lowbit()函数, 返回二进制数最右边的一个1及其后面的0
#define lowbit(x) ((x) & (-x))

原理: 计算机中有符号数一般通过补码存储, $-x$ 为 $x$ 按位取反再$+1$, 从右往左直至第一个 $1$ 都相同, 再往左的位数全部相反, 两者按位与之后恰好得到二进制数最右边的一个 $1$ 及其后面的 $0$ .

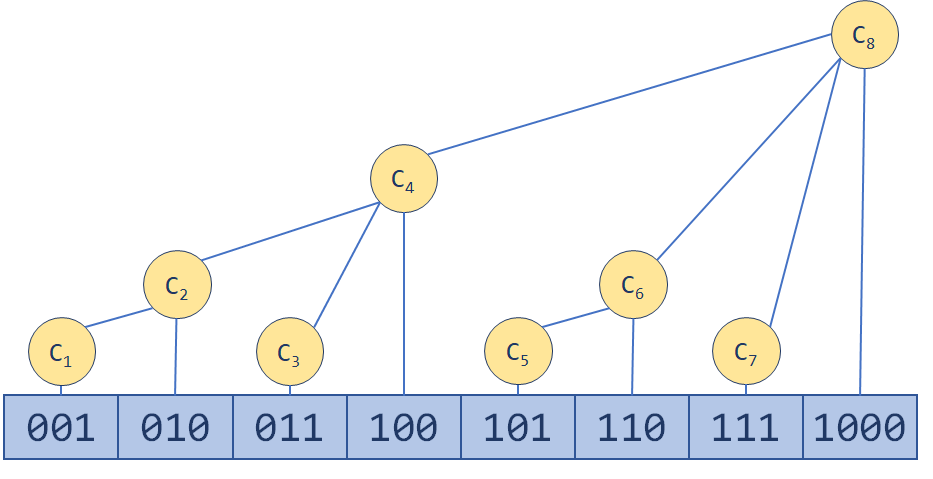
  • 单点修改 首先需要明白 $C_i$ 维护了区间 $(A_i-lowbit(Ai), Ai]$ , 对于某一点进行修改, 需要相应地修改包含它的所有区间. 这一修改过程, 实质上相当于不停地给节点下标加上其 $lowbit()$ 值. 
//单点修改&初始化操作, 将tree[i]增加x, 
inline void update(int i, int x)
{
    for (int pos = i; pos < MAXN; pos += lowbit(pos))
        tree[pos] += x;
}
  • 区间查询 我们考虑前 $i$ 项和, 将 $i$ 转化成二进制, 前 $i$ 项和恰等于对 $(j-lowbit(j), j]$ 区间累加(每次去掉最右边一个 $0$).
inline int query(int n)
{
    int ans = 0;
    for (int pos = n; pos; pos -= lowbit(pos))
        ans += tree[pos];
    return ans;
}

对于树状数组, 每次操作涉及的区间数不超过 $log_2MAXN$, 对于单点修改和区间查询而言, 时间复杂度都为 $O(logn)$ .

↑