Table of Contents

网络表示法 #

网络的概念 #

网络是一个图 $G = (N, A)$ , $N$ 是节点集, $A$ 是边集. 网络具有如下的特点:

边有向
图 $G$ 是简单图

网络中可能会有两个特殊点, 分别是入度为 $0$ 的点和出度为 $0$ 的点.

网络的存储 #

我们需要存储:

网络的拓扑结构
网络相关的数据, 包括
- 边权

为了表示拓扑结构, 有这些方法:

关联矩阵 (Node-arc incidence matrix)
邻接矩阵 (Node-node adjacency matrix)
邻接表 (Adjacency list)
星式表示法 (Star (array) representations)

关联矩阵 #

关联矩阵的行坐标为节点, 列坐标为边, 矩阵元素值为 $0$ 代表边与节点无关联, 为 $1$ 代表节点为边的出发点, 为 $-1$ 代表节点为边的目标点.

通过定义, 可以得到如下的性质:

每一列有且仅有一个 $1$ 和一个 $-1$
每一行 $1$ 的数量等于节点的出度
每一行 $-1$ 的数量等于节点的入度

如果有 $n$ 个节点, $m$ 条边, 总共需要 $nm$ 的空间, 其中存储有效信息的是 $2m$ , 利用率为 $\frac{2}{n}$ . 显然, 在 $n$ 增长时, 利用率会变得越来越低.

邻接矩阵 #

邻接矩阵行和列坐标都是节点, 如果存在从行节点到列节点的边, 这一格的值为 $1$ . 如果有 $n$ 个节点, $m$ 条边, 总共需要 $n^2$ 的空间, 其中存储有效信息的是 $m$ , 利用率为 $\frac{m}{n^2}$ . 如果是稀疏网络, $m = kn$ , 利用率是 $k / n$ ; 如果是稠密网络, $m = n^2 - n$ , 利用率是 $\frac{n - 1}{n}$ . 因此邻接矩阵适合稠密网络, 对于稀疏网络效果不佳.

邻接表 #

用链表节点数组来存储图. 以一个节点为出发点的所有邻接点构成该节点为头节点的链表后继.

如果有 $n$ 个节点, $m$ 条边, 需要 $n$ 个 null, $m$ 个指针, $m$ 个邻接点空间, 以及 $n$ 个头节点, 总计 $2n + 2m$ 的空间. 邻接表法的问题是

指针需要空间
指针可能在代码编写上带来麻烦

星式表示法 #

定义 $A(i) = {l\in N\vert (i, l)\in Arc}$ 为节点 $i$ 的后继点集, $B(i) = {l\in N\vert (l, i)\in Arc}$ .

星式表示法和邻接表很相似, 区别在于

边以数组的形式存储, 而非链表
边是有序的

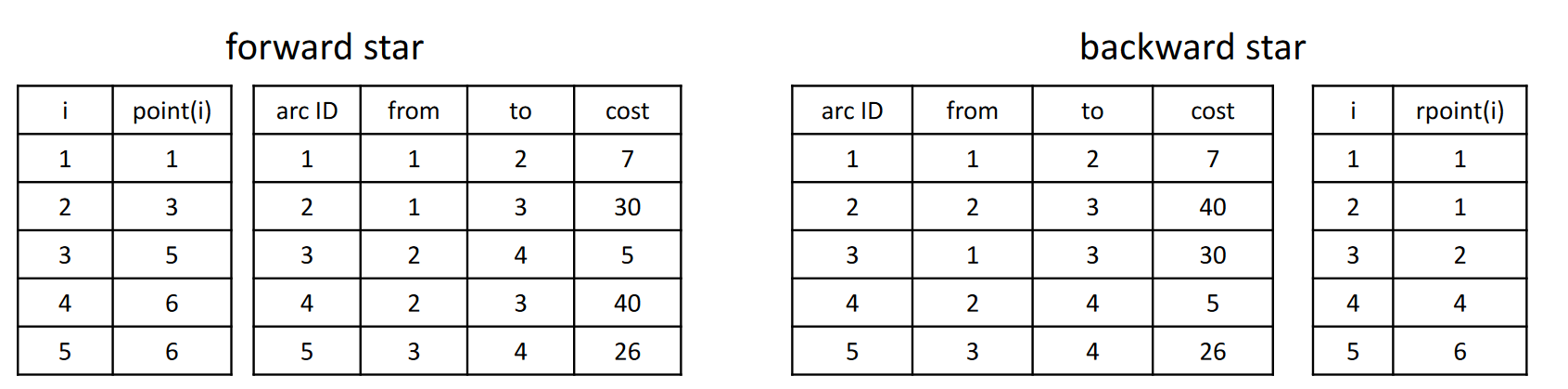
前向星 #

我们按如下顺序给边编号: 以节点 $1$ 为出发点的边, 以节点 $2$ 为出发点的边, …

可以用边编号, 出发点, 到达点, 边权四列构成的矩阵来代表一个图.

记 $point(i)$ 为从节点 $i$ 出发的边的最小编号. 可以通过如下的方式计算所有的 $point(i)$ :

point(1) ← 1
point(n + 1) ← m + 1
For j ← n to 2
    If there are arcs leaving node j
        point(j) ← the smallest arc ID leaving j
    Else
        point(j) ← point(j + 1)

节点 $i$ 的出度 $= point(i + 1) - point(i)$ , 因为节点 $i$ 发出的边的编号是 $point(i), …, point(i + 1) - 1$ .

后向星 #

我们按如下顺序给边编号: 以节点 $1$ 为到达点的边, 以节点 $2$ 为到达点的边, …

其它与前向星类似, 这里定义了 $rpoint(i)$ 函数, 也有类似的计算方法:

rpoint(1) ← 1
rpoint(n + 1) ← m + 1
For j ← n to 2
    If there are arcs entering node j
        point(j) ←the smallest arc ID entering j
    Else
        point(j) ← point(j + 1)

两种表示法的关联 #

前向星的着手点在于出度, 后向星在于入度, 分别对应了 $A(i)$ 与 $B(i)$ .

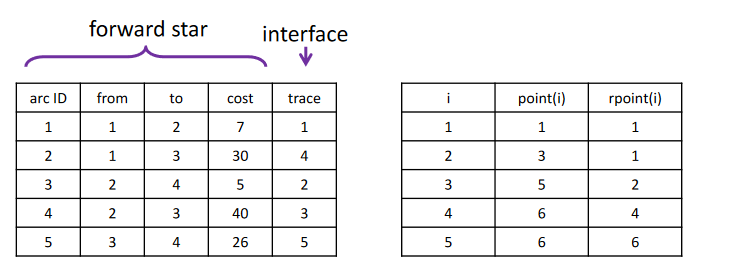
为了建立两者之间的关联, 通常可以

先建立前向星的表示法
增加一个大小为 $m$ 的接口数组 (interface array), 记为 $trace$
前向星表示中的边的属性 $trace(i)$ 对应后向星表示中的它的边编号 $i$ .